Memory Scaling on Haswell CPU, IGP and dGPU: DDR3-1333 to DDR3-3000 Tested with G.Skill
by Ian Cutress on September 26, 2013 4:00 PM ESTOne side I like to exploit on CPUs is the ability to compute and whether a variety of mathematical loads can stress the system in a way that real-world usage might not. For these benchmarks we are ones developed for testing MP servers and workstation systems back in early 2013, such as grid solvers and Brownian motion code. Please head over to the first of such reviews where the mathematics and small snippets of code are available.
3D Movement Algorithm Test
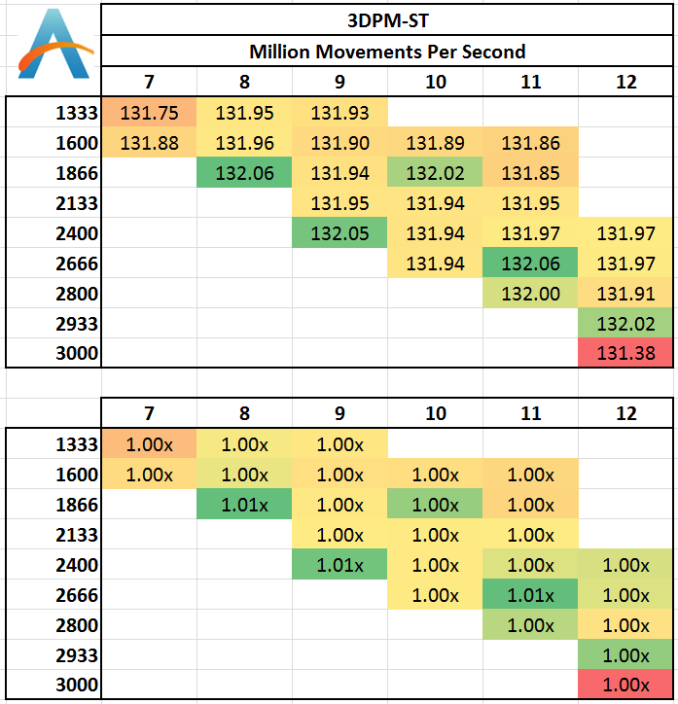
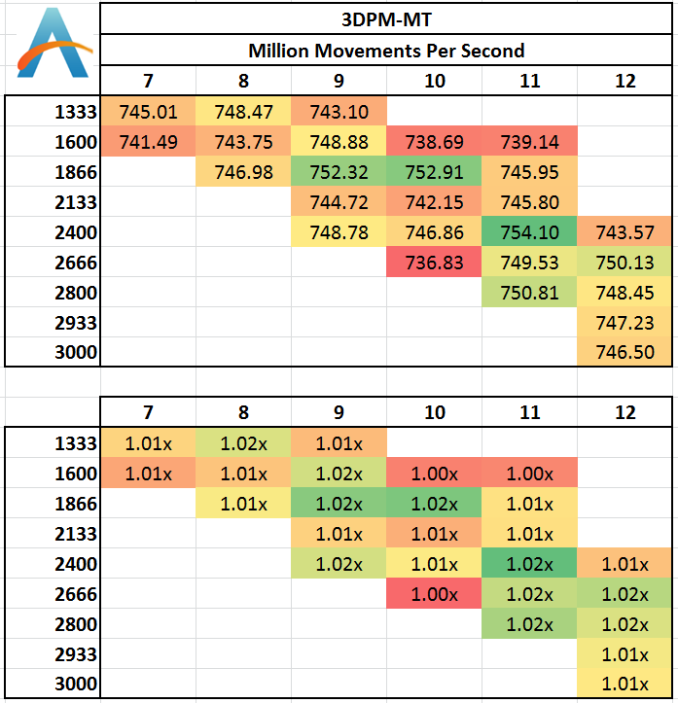
The algorithms in 3DPM employ uniform random number generation or normal distribution random number generation, and vary in various amounts of trigonometric operations, conditional statements, generation and rejection, fused operations, etc. The benchmark runs through six algorithms for a specified number of particles and steps, and calculates the speed of each algorithm, then sums them all for a final score. This is an example of a real world situation that a computational scientist may find themselves in, rather than a pure synthetic benchmark. The benchmark is also parallel between particles simulated, and we test the single thread performance as well as the multi-threaded performance. Results are expressed in millions of particles moved per second, and a higher number is better.
Single threaded results:
For software that deals with a particle movement at once then discards it, there are very few memory accesses that go beyond the caches into the main DRAM. As a result, we see little differentiation between the memory kits, except perhaps a loose automatic setting with 3000 C12 causing a small decline.
Multi-Threaded:
With all the cores loaded, the caches should be more stressed with data to hold, although in the 3DPM-MT test we see less than a 2% difference in the results and no correlation that would suggest a direction of consistent increase.
N-Body Simulation
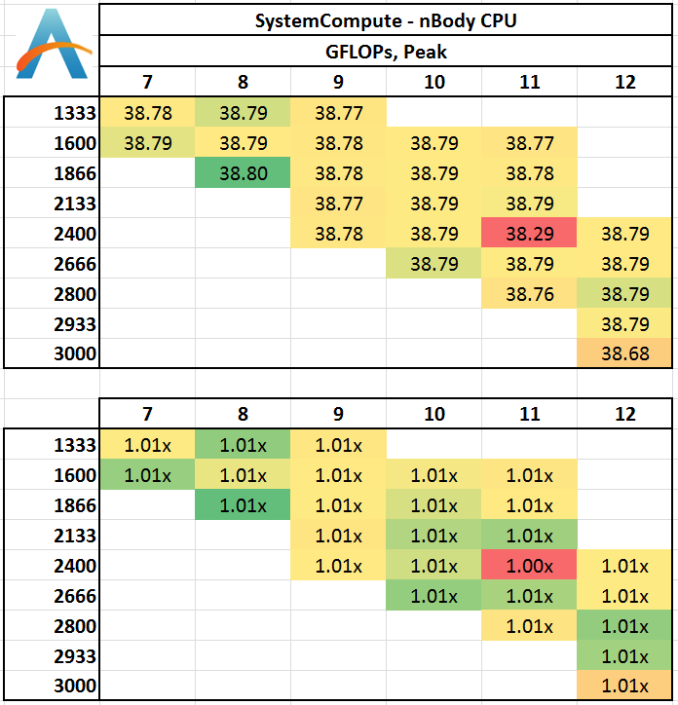
When a series of heavy mass elements are in space, they interact with each other through the force of gravity. Thus when a star cluster forms, the interaction of every large mass with every other large mass defines the speed at which these elements approach each other. When dealing with millions and billions of stars on such a large scale, the movement of each of these stars can be simulated through the physical theorems that describe the interactions. The benchmark detects whether the processor is SSE2 or SSE4 capable, and implements the relative code. We run a simulation of 10240 particles of equal mass - the output for this code is in terms of GFLOPs, and the result recorded was the peak GFLOPs value.
Despite co-interaction of many particles, the fact that a simulation of this scale can hold them all in caches between time steps means that memory has no effect on the simulation.
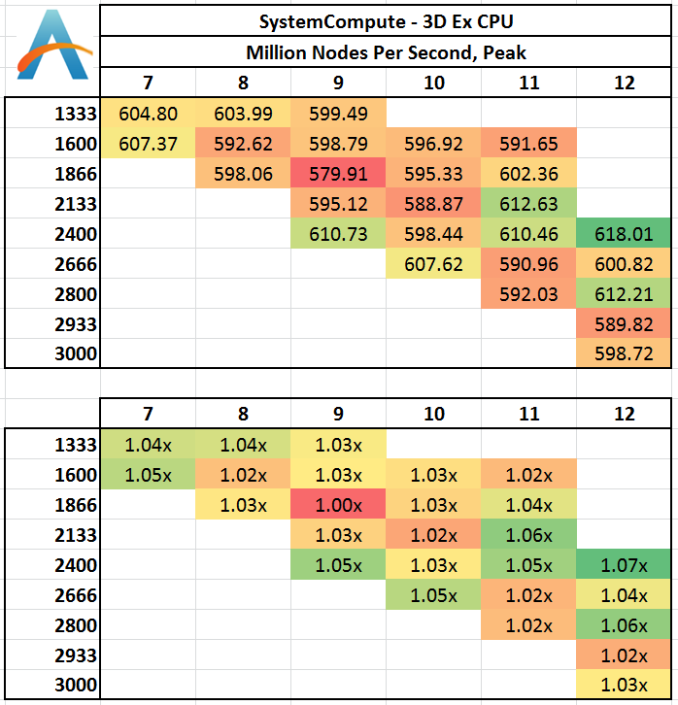
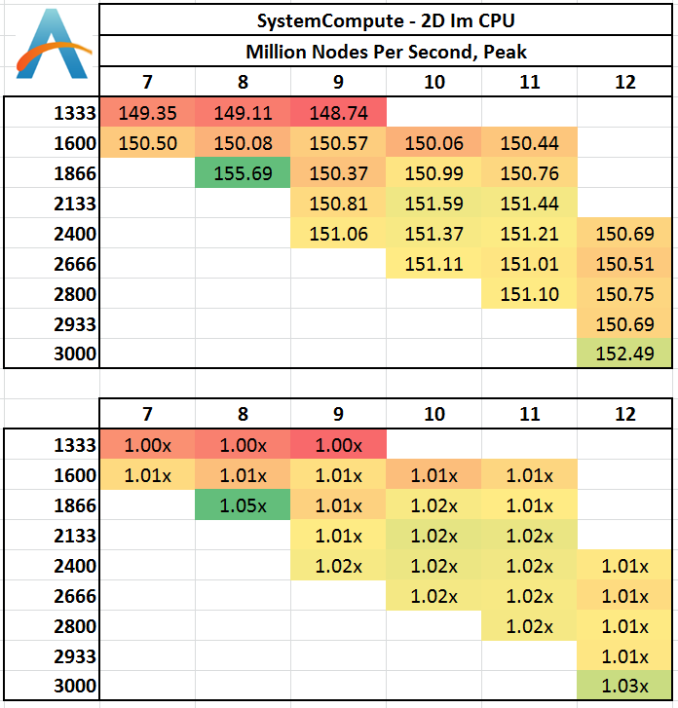
Grid Solvers - Explicit Finite Difference
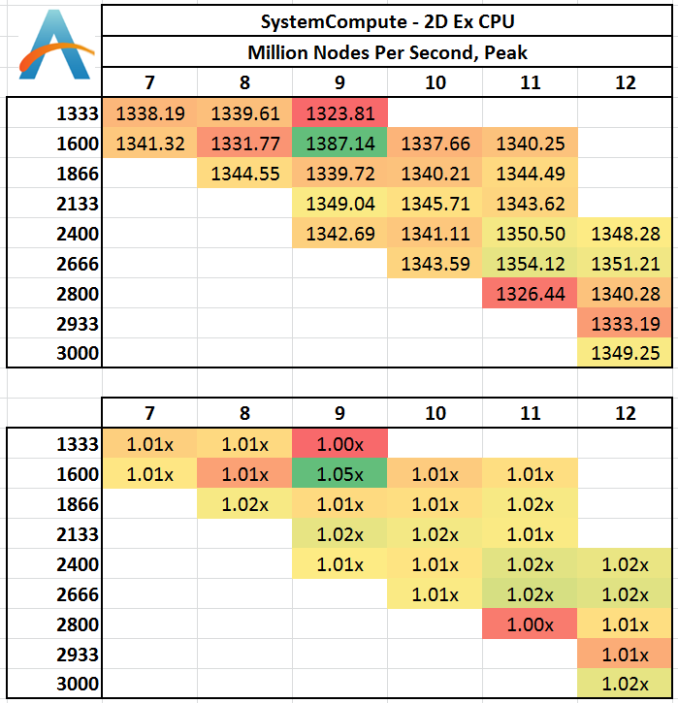
For any grid of regular nodes, the simplest way to calculate the next time step is to use the values of those around it. This makes for easy mathematics and parallel simulation, as each node calculated is only dependent on the previous time step, not the nodes around it on the current calculated time step. By choosing a regular grid, we reduce the levels of memory access required for irregular grids. We test both 2D and 3D explicit finite difference simulations with 2n nodes in each dimension, using OpenMP as the threading operator in single precision. The grid is isotropic and the boundary conditions are sinks. We iterate through a series of grid sizes, and results are shown in terms of ‘million nodes per second’ where the peak value is given in the results – higher is better.
Two-Dimensional Grid:
In 2D we get a small bump over at 1600 C9 in terms of calculation speed, with all other results being fairly equal. This would statistically be an outlier, although the result seemed repeatable.
Three Dimensions:
In three dimensions, the memory jumps required to access new rows of the simulation are far greater, resulting in L3 cache misses and accesses into main memory when the simulation is large enough. At this boundary it seems that low CAS latencies work well, as do memory speeds > 2400 MHz. 2400 C12 seems a surprising result.
Grid Solvers - Implicit Finite Difference + Alternating Direction Implicit Method
The implicit method takes a different approach to the explicit method – instead of considering one unknown in the new time step to be calculated from known elements in the previous time step, we consider that an old point can influence several new points by way of simultaneous equations. This adds to the complexity of the simulation – the grid of nodes is solved as a series of rows and columns rather than points, reducing the parallel nature of the simulation by a dimension and drastically increasing the memory requirements of each thread. The upside, as noted above, is the less stringent stability rules related to time steps and grid spacing. For this we simulate a 2D grid of 2n nodes in each dimension, using OpenMP in single precision. Again our grid is isotropic with the boundaries acting as sinks. We iterate through a series of grid sizes, and results are shown in terms of ‘million nodes per second’ where the peak value is given in the results – higher is better.
2D Implicit:
Despite the nature if implicit calculations, it would seem that as long as 1333 MHz is avoided, results are fairly similar. 1866 C8 being a surprise outlier.










89 Comments
View All Comments
DanNeely - Thursday, September 26, 2013 - link
A suggestion for future articles of this type. If the results mostly show that really slow memory is bad but above that it doesn't really matter, normalizing data with a reasonably priced option that performs well as 1.0 might make clearer. ex for the current results put 1866-C9 as 1.0, and having 1333 as .9x and 3000 as 1.02. I think this would would help drive home that you're hitting diminishing returns on the cheap stuff.superjim - Thursday, September 26, 2013 - link
It looks like the days of 1600 C9 being the standard are over however the Hynix fire isn't helping faster memory prices any. 4-5 months ago you could get 2x 4GB of 1600 C9 for $30-35 bucks.Belial88 - Tuesday, October 1, 2013 - link
That's because just like when HDD prices skyrocketed due to the 2011 Thailand Flood, RAM prices have skyrocketed due to the 2013 Hynix Factory Fire. Prices had started to rise around early 2013 due to market consolidation and some other electronics (tablet, console, etc market needs), nothing huge, and they were actually starting to drop until the factory fire.As for 1600 C9 being some sort of standard, well, what Intel/AMD specifies as their rated RAM speed is no more useful than what they specify their CPU speed, as we know the chip can go way above that. JPeople who are savvy and know how to buy RAM, can buy RAM easily capable of 2400mhz CL8 by researching the RAM IC.
PSC/BBSE is easily capable of 2400mhz CL8 and generally costs ~$60 per 8gb (ie similar to the cheapest ddr3 ram). You can find some Hynix CFRs (double sided, unlike MFR, meaning they don't hit the high mhz numbers, but way better 24/7 performance clock for clock, kinda like dual channel vs single channel) for around $65, like the Gskill Ripjaws X 2400CL11 (currently like $75 on newegg), which will easily do ~2800mhzCL13.
RAM speed has always made an impact, the problem with reviews like the above is assuming you can't overclock RAM, and have to pay for it. In reality there is only ~5 different types of RAM (and a few subtypes). If you are smart and purchase Hynix, Samsung instead of Spektek, Qimonda, you can get RAM that easily does 2400mhz+ for the same or simliar price as the cheapest spekteks. If you assume that going from 1600 to 2400 will cost you $100+, of course it's a ripoff...
But if you buy, say, some Gskill Pi's 1600mhz for bargain bin, and overclock them to 2400CL8, you gain a good 10+ fps for almost nothing, and that's an awesome value. All RAM is just merely rebranded Spektek/Qimonda/PSC/BBSE/Hynix/Samsung, ie the same RAM is sold as 1600 CL9, 1600 CL8 1.65v, 1866 CL10, 2000CL11, 2133 CL12, etc ad nauesum.
vol7ron - Monday, September 30, 2013 - link
Relational results are helpful -I think they've been added since your comment- but I also like to see the empirical data as is also being listed.I know these things are currently being done in this article, I just want to make it a point not to make the decision to use one or the other, but both, again in the future.
vol7ron - Monday, September 30, 2013 - link
As an amendment, I want to add that the thing I would change in the future is the colors used. The spectrum should be green:good red:hazardous/bad. If you have something at 1.00x, perhaps that should be yellow, since it's the neutral starting position.alfredska - Monday, September 30, 2013 - link
Yes, this is some pretty basic stuff. It seems there's bouncing back and forth between green = good/bad right now. The author needs to stick to a convention throughout the article. I'm not really of the opinion that green and red are the best choices, but at least if a convention is used I can train my eyes.xTRICKYxx - Thursday, September 26, 2013 - link
It would be cool to see other IGP's including Iris Pro or HD 5000. Also, Richland may see slightly more than the 5% Haswell's HD 4600 has.Khenglish - Thursday, September 26, 2013 - link
I would expect richland/trinity to have larger gains since the IGP has access to only 4MB cache instead of 6MB or 8MB found on intel processors.yoki - Thursday, September 26, 2013 - link
hi, you said that the order of importance place amount of memory & their placement is most importance, but not a clue regarding how this scale in real world... for example i have 1600mhz 7Cl 6GB RAM in a x58 system,,,,should i upgrade it to 12GB ... how much i'll gain from thatIanCutress - Thursday, September 26, 2013 - link
That's ultimately up for the user to determine based on workload, gaming style, etc. I'd always suggest playing it safe, so if you plan on doing anything that would tax a system, 12gb might be a safe bet. That's X58 though, this is talking about Haswell, whose memory controller can take this high end kits ;)